Description
Week 6: Confidence Interval
| Week | Assignments | Due Date |
| Week 6 | Graded Discussion | Suggested Due Date—
Initial Post: Wednesday of Week 6
Due Date— Responses: Sunday of Week 6 [Have two posts on two different days] |
| Knewton Homework Assignments
Confidence Interval for Mean – Population Standard Deviation Known Confidence Intervals – Empirical Rule Estimating Sample Size for a Population Proportion Point Estimates, Margins of Error, and Confidence Intervals Understanding Confidence Intervals – Excel |
Sunday of Week 6 | |
| Week 6 Quiz |
—————-
Week 6 Assignment – Confidence Interval for Mean – Population Standard Deviation Known (2)
Activity 1
Question
Suppose the scores of a standardized test are normally distributed. If the population standard deviation is 4 points, what minimum sample size is needed to be 95% confident that the sample mean is within 1 point of the true population mean?
Use the table above for the z-score, and be sure to round up to the nearest integer.
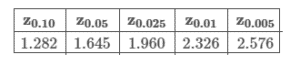
Answer
Access the entire solutions for this week (top graded solutions) by clicking the ‘Buy’ button.
Activity 2
Question
Suppose the weights, in pounds, of the dogs in a city are normally distributed. If the population standard deviation is 3 pounds, what minimum sample size is needed to be 95% confident that the sample mean is within 1 pound of the true population mean?
Use the table above for the z-score, and be sure to round up to the nearest integer.
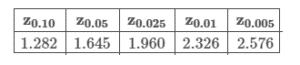
Answer
Access the entire solutions for this week (top graded solutions) by clicking the ‘Buy’ button.
Activity 3
Question
Suppose the finishing times for cyclists in a race are normally distributed. If the population standard deviation is 16 minutes, what minimum sample size is needed to be 90% confident that the sample mean is within 5 minutes of the true population mean?
Use the table above for the z-score, and be sure to round up to the nearest integer.
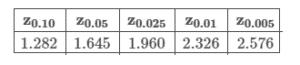
Provide your answer below:
Answer
Access the entire solutions for this week (top graded solutions) by clicking the ‘Buy’ button.
Activity 4
Question
Suppose the germination periods, in days, for grass seed are normally distributed. If the population standard deviation is 3 days, what minimum sample size is needed to be 90% confident that the sample mean is within 1 day of the true population mean?

Use the table above for the z-score, and be sure to round up to the nearest integer.
Answer
Access the entire solutions for this week (top graded solutions) by clicking the ‘Buy’ button.
Activity 5
Question
The length, in words, of the essays written for a contest are normally distributed with a population standard deviation of 442 words and an unknown population mean. If a random sample of 24 essays is taken and results in a sample mean of 1330 words, find a 99% confidence interval for the population mean.

You may use a calculator or the common z values above.
Answer
Access the entire solutions for this week (top graded solutions) by clicking the ‘Buy’ button.
Activity 6
Question
Suppose the scores of a standardized test are normally distributed. If the population standard deviation is 2 points, what minimum sample size is needed to be 90% confident that the sample mean is within 1 point of the true population mean?
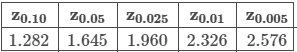
Use the table above for the z-score, and be sure to round up to the nearest integer.
Answer
Access the entire solutions for this week (top graded solutions) by clicking the ‘Buy’ button.
Activity 7
Question
The lengths, in inches, of adult corn snakes are normally distributed with a population standard deviation of 8 inches and an unknown population mean. A random sample of 25 snakes is taken and results in a sample mean of 58 inches.
Identify the parameters needed to calculate a confidence interval at the 99% confidence level. Then find the confidence interval.
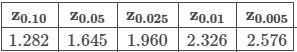
You may use a calculator or the common z values above.
Answer
Access the entire solutions for this week (top graded solutions) by clicking the ‘Buy’ button.
Activity 8
Question
The lengths, in inches, of adult corn snakes are normally distributed with a population standard deviation of 8 inches and an unknown population mean. A random sample of 25 snakes is taken and results in a sample mean of 58 inches.
What is the correct interpretation of the confidence interval?
Select the correct answer below:
- We can estimate with 99% confidence that the true population mean length of adult corn snakes is between 53.88 and 62.12 inches.
- We can estimate with 99% confidence that the sample mean length of adult corn snakes is between 53.88 and 62.12 inches.
- We can estimate that 99% of adult corn snakes will have a length that is between 53.88 and 62.12 inches
Answer
Access the entire solutions for this week (top graded solutions) by clicking the ‘Buy’ button.
Activity 9
Question
The weights, in pounds, of dogs in a city are normally distributed with a population standard deviation of 2 pounds and an unknown population mean. A random sample of 16 dogs is taken and results in a sample mean of 28 pounds.
Identify the parameters needed to calculate a confidence interval at the 90% confidence level. Then find the confidence interval.
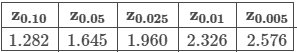
You may use a calculator or the common z values above.
Answer
Access the entire solutions for this week (top graded solutions) by clicking the ‘Buy’ button.
Activity 10
Question
The weights, in pounds, of dogs in a city are normally distributed with a population standard deviation of 2 pounds and an unknown population mean. A random sample of 16 dogs is taken and results in a sample mean of 28 pounds.
What is the correct interpretation of the confidence interval?
Select the correct answer below:
- We can estimate that 90% of the dogs in the city have a weight that lies between 27.18 and 28.82 pounds.
- We can estimate with 90% confidence that the sample mean weight of dogs in the city is between 27.18 and 28.82 pounds.
- We can estimate with 90% confidence that the true population mean weight of dogs in the city is between 27.18 and 28.82 pounds.
Answer
Access the entire solutions for this week (top graded solutions) by clicking the ‘Buy’ button.
Activity 11
Question
Suppose the heights of seasonal pine saplings are normally distributed. If the population standard deviation is 14 millimeters, what minimum sample size is needed to be 95% confident that the sample mean is within 4 millimeters of the true population mean?
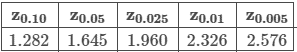
Use the table above for the z-score, and be sure to round up to the nearest integer.
Answer
Access the entire solutions for this week (top graded solutions) by clicking the ‘Buy’ button.
Activity 12
Question
The population standard deviation for the scores of a standardized test is 4 points. If we want to be 90% confident that the sample mean is within 1 point of the true population mean, what is the minimum sample size that should be taken?
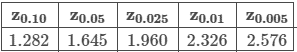
Use the table above for the z-score, and be sure to round up to the nearest integer.
Answer
Access the entire solutions for this week (top graded solutions) by clicking the ‘Buy’ button.

![[Top Answer] MATH225N - WeeK 6 Assignment Confidence Interval for Mean – Population Standard Deviation Known (2)](https://prolifictutors.com/wp-content/uploads/2022/07/Top-Answer-MATH225N-WeeK-6-Assignment-Confidence-Interval-for-Mean-–-Population-Standard-Deviation-Known-2.jpg)

![[Solution] - NR305 - Week 5 Discussion: Debriefing of Week 4 iHuman Neurovascular Assessment (Graded)](https://prolifictutors.com/wp-content/uploads/2022/06/Solution-NR305-Week-5-Discussion-Debriefing-of-Week-4-iHuman-Neurovascular-Assessment-Graded.png)
![[Solution] - NR305 - Week 8 Discussion: Reflection on End of Life Care (Graded)](https://prolifictutors.com/wp-content/uploads/2022/06/Solution-NR305-Week-8-Discussion-Reflection-on-End-of-Life-Care-Graded.png)



Reviews
There are no reviews yet.